Dal blog di Scott McKinney una bella visione della matematica dei mappamondi
 In un precedente post dedicato alla relazione fra geometria euclidea e navigazione Scott ha mostrato come la geometria euclidea è adatta a svolgere calcoli su una superficie piana in quanto, come sappiamo dalle Elementari, se si estendono indefinitamente due linee parallele non si incontreranno mai.
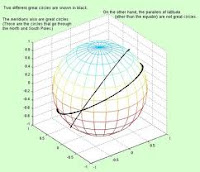
In un precedente post dedicato alla relazione fra geometria euclidea e navigazione Scott ha mostrato come la geometria euclidea è adatta a svolgere calcoli su una superficie piana in quanto, come sappiamo dalle Elementari, se si estendono indefinitamente due linee parallele non si incontreranno mai.Su una sfera, invece, se estendiamo due linee parallele (ovvero due cerchi) questi finiranno per intersecarsi.
Una conseguenza della differenza fondamentale tra superfici piane e superfici sferiche è che qualsiasi rappresentazione planare della Terra, come una mappa, manifesterà necessariamente alcune distorsioni. Le differenze tra geometria di una sfera e geometria di una superficie piana appaiono evidenti quando cerchiamo di proiettare i continenti della Terra su una mappa. Per capirlo basta disegnare la forma dei continenti con un pennarello sulla superficie di un'arancia, poi la si sbuccia delicatamente e si prova ad appiattirla.
Nel post dell'8 Gennaio 2013 - "Non-Euclidean Geometry and Map-Making" - Scott esamina la matematica che si trova dietro queste proiezioni nelle diverse tipologie di mappe, come quella Marcatore (adatta al tracciamento di rotte navali e aree) e quella Galls-Peters (fedele alle proporzioni dei continenti.
Andrea Mameli www.linguaggiomacchina.it 18 Gennaio 2013
“La misura del mondo” Gauss e Humboldt, due mostri sacri per un best seller (L'Unione Sarda, 11 Luglio 2006)
- I sentieri dei pastori, i fuoristrada e le mappe aborigene che diventano quadri (Linguaggio Macchina, 9 Luglio 2011)
- Da Belvì a Honk Kong. Laboratori, mappe, scambi culturali: la ricerca di Alessandro Carboni (Linguaggio Macchina, 23 Giugno 2012)




Commenti